线性表
说明: 在此,我将栈和队列归为线性表特殊的存在,我们一般讲的线性表指顺序表和链表。
-
定义:具有相同特性的数据元素的一个有限序列。
-
线性表(顺序表+链表)抽象数据类型描述:
ADT List{ date: 数据对象集合{a1, a2,..., an}, 除 a1 和 an , 其他元素都有前赴后继,数据关系为一对一。 基本操作(operation): InitList(&L): 初始化操作,建立空列表L ListEmpty(L):若线性表为空,返回true,否则false ClearList(&L): 清空线性表 ListLength(L): 返回线性表长度 GetElem(L, i, &e): 将线性表中第i个位置返回给e LocateElem(L, e): 返回第一个e所在位置,否则返回0表示失败 ListInsert(&L, i, e): 将e插入到位置i,length++ ListDelete(&L, i, &e): 将位置i删除,返回e, length-- // 修改对象,可以用&,也可以用指针 * //‘.’和‘->’ 的区别就是在一个是普通成员引用,一个是指针引用 }
顺序表
-
线性表的顺序存储结构(顺序表):
-
借助数组类型实现顺序表,注意插入位置i 与数组下表的区别(相差1),顺序表是有下标的;
-
设计分三个文件:1个头文件(抽象声明)和2个cpp文件,一个是头文件具体代码实现过程,一个是main()调用。
-
数组大小、及结构体类型:
#define MaxSize 100 //分配线性表最大长度 typedef int DateType; //声明元素类型 typedef struct { DateType data[MaxSize]; //存放线性表数据 int length; }SqList; // SqList为用户定义的线性表类型
-
-
顺序表的应用:
要求:Time complexity : O(n) Space complexity : O(1)
-
假设有一顺序表,设计一个算法,删除所有值等于x的元素;
void Test1(SqList &L, DataType e) { DataType k = 0; for (int i = 0; i < L.length; i++) if (L.data[i] != e) L.data[k++] = L.data[i]; L.length = k; }
-
有一顺序表,以第一个元素为基准,将所有小于等于它的元素移动到它前面,大于的移动到后面;
//第一种 void Test2(SqList &L) { DataType value = L.data[0]; DataType i = 0, j = L.length - 1; while (i < j) //从顺序表两端交替向中间扫描 { //从右到左找到小于等于value的值a while (i < j && L.data[j] > value) j--; //从左到右找到大于value的值b while (i < j && L.data[i] <= value) i++; //如果b在a左边,交换两者 if(i < j) swap(L.data[i], L.data[j]); } swap(L.data[0], L.data[i]); } //第二种 void Test2(SqList &L) { DataType value = L.data[0]; DataType i = 0, j = L.length - 1; while (i < j) { //从右到左找到小于等于value的值a while (i < j && L.data[j] > value) j--; L.data[i] = L.data[j]; //从左到右找到大于value的值b while (i < j && L.data[i] <= value) i++; L.data[j] = L.data[i]; } L.data[i] = value; } /* 上面两种算法就好比将{a,b,c}->{b,c,a}; 第一种是先swap(a,b),内部交换了3次,得到{b,a,c}再swap(a,c),总共交换6次; 第二种相当于:tmp=a,a=b,b=c,c=tmp; */
-
有一顺序表,将所有奇数移动到偶数前面;
//类似于第2题第一种解法的思路 void Test3(SqList &L) { DataType value = L.data[0]; DataType i = 0, j = L.length - 1; while (i < j) //从顺序表两端交替向中间扫描 { //从右到左找到奇数a while (i < j && L.data[j] %2 ==0) j--; //从左到右找到偶数b while (i < j && L.data[i] %2 != 0) i++; //如果b在a左边,交换两者 if (i < j) swap(L.data[i], L.data[j]); } }
-
链表
-
线性表的链式存储结构(链表):
链表不同于顺序表,它的每个结点由数据域和指针域组成,没有小标而且它是动态分划空间的;
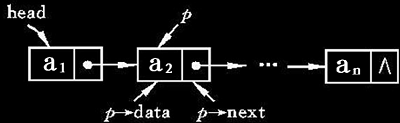
图片所展示的就是头指针(head)、头结点、尾节点;
-
链表的实现
struct Node //Node为结点类型名 { DataType data; //data代表数据元素 struct Node *next; //next为指向下一结点的指针 }; //其他的接口基本与顺序表一致,所不同的只是代码的实现过程 //初始化单链表 int InitList(Node *&H) { //H为指向单链表的头指针 H = new Node; if (!H) { cout << "初始化错误" << endl; return 0; } H->next = NULL; return 1; } /*插入最重要是查找前驱位置,可定义i=0;当i=pos时,插入即可;移动时,要注意拼接顺序*/ int ListInsert(Node *H, int pos, DataType item); -
链表的应用
#栈和队列是两种重要的线性结构。从数据结构角度看,栈和队列也是线性表,其特殊性在于
栈和队列的基本操作是线性表操作的子集,它们是操作受限的线性表。但从数据类型角度看,
它们是和线性表大不相同的两类重要的抽象数据类型。
#线性表有顺序存储和链式存储,栈和队列是特殊的线性表,同样有这两种;
栈 (Stack)
-
定义:栈(Stack)是限定只能在表的一端进行插入和删除操作的线性表。特点:后进先出(LIFO)
-
抽象数据类型描述:
ADT Stack{ Data 数据对象集合,和线性表一样,具有前仆后继关系 基本操作: InitStack( &S ) 构造一个空栈S StackEmpty( S ) 若S为空栈,则返回TRUE,否则返回FALSE StackLength( S ) 返回S的数据元素个数,即栈的长度 GetTop( S, &e ) 获取S的栈顶元素赋值给e Push( &S, e ) 插入元素e为新的栈顶元素 Pop( &S, &e ) 删除S的栈顶元素,并用e返回其值 DestroyStack ( &S ) 初始条件:栈S已存在。 操作结果:销毁栈S。 ClearStack( &S ) 初始条件:栈S已存在。 操作结果:将S清为空栈。 }
-
栈的应用
-
回文:将对象s是进栈,Pop出后与 s[i] 比较
int IsReverse(char * s) { SNode* top ; InitStack(top); char t; for (int i = 0; i < strlen(s); i++) Push(top, s[i]); int i = 0; while (StackEmpty(top)!=1) { Pop(top, t); if (t != s[i]) return 0; else i++; } return 1; }
-
进制转换(十进制->其他进制):
//利用栈实现 void Convert(int num, int d) { //num为待转换数,d为进制 SqStack S; ElemType result; int r; //余数 char ch[] = "0123456789ABCDEF"; //进制所使用的数字 InitStack(S); while (num != 0) { r = num%d; //取余数r Push(S, ch[r]); //余数入栈 num = num / d; //利用商进行下一次运算 } while (StackEmpty(S) != 1) { Pop(S, result); cout << result-'0'; } }
//利用递归实现
void Convert(int num, int d)
{
char ch[] = "0123456789ABCDEF"; //进制所使用的数字
if(num == 0)
cout<<"结果: ";
else{
Convert(num/d,d);
cout<< ch[num % d];
}
}
```
-
递归: This link
-
迷宫问题:
/* #描述: 迷宫可以以二维数组来存储表示。0表示通路,1表示障碍。注意这里规定移动可以从上、下、左、右四方方向移动。 坐标以行和列表示,均从0开始,给定起点(0,0)和终点(4,4),迷宫表示如下: int maze[5][5]={ {0,0,0,0,0}, {0,1,0,1,0}, {0,1,1,0,0}, {0,1,1,0,1}, {0,0,0,0,0} }; 在此我们只要求其中一条路径即可 */
-
四则运算表达式求值:
#思路:先将我们平时的中缀表达式转化为后缀表达式,然后计算后缀表达式; 后缀表达式计算:9 3 1 - 3 * + 10 2 / + #规则:从左到右遍历,遇到数字就进栈,遇到符号,就将处于栈顶两个数字出栈, 进行运算,运算结果进栈,一直到最终获得结果。 结果很显然是20,可是怎么转换为后缀表达式? 即: “ 9+(3-1)*3+10/2 ” --> “ 9 3 1 - 3 * + 10 2 / + ” #规则: 从左到右遍历,遇到数字输出,若是遇到符号,判断其与栈顶的优先级, 是右括号或者优先级不高于栈顶符号,则栈顶元素依次输出,并将当前元素进栈 (也要判断优先级),一直到最终输出后缀表达式为止。
具体实现代码在库Data-Structures
队列(Queue)
-
定义:顾名思义,特点就是只能在队头删除,队尾插入;符合先进先出(FIFO)
-
抽象数据类型描述:
ADT Queue{ Data 数据对象集合,和线性表一样,具有前仆后继关系 基本操作: InitQueue( &Q ) 构造一个空队列Q QueueEmpty( Q ) 若Q为空队列,则返回TRUE,否则返回FALSE QueueLength( Q ) 返回Q的数据元素个数,即队列的长度 GetHead( Q, &e ) 初始条件:队列Q已存在且非空 操作结果:用e返回Q的队头元素 EnQueue( &Q, e ) 初始条件:队列Q已存在 操作结果:插入元素e为Q的新的队尾元素 DeQueue( &Q, &e ) 初始条件:队列Q已存在且非空 操作结果:删除Q的队头元素,并用e返回其值 DestroyQueue ( &Q ) 初始条件:队列Q已存在 操作结果:销毁队列Q ClearQueue ( &Q ) 初始条件:队列Q已存在 操作结果:将Q清为空队列 }
-
队列顺序存储
队列顺序存储实现存在着要么大量移动元素问题 OR 假溢出问题;因此我们采用将队头和队尾头尾相接,称为循环队列。需要说明的是,front指针指向队头结点,rear指针指向队尾结点,而‘rear->next’指向队尾结点指针域。
循环队列的实现存在着队列状态判断问题,当“front==rear”时,到底是队空还是队满?我们无法判断,因此需要保留一个元素空间(当然这只是其中一种高效的处理方式),也就是说队列满时,数组中还有一个空闲单元。
其中比较重要的两个判断式:
队列满的条件:(rear+1)%QueueSize == front
队列长度求法:(rear - front + QueueSize ) % QueueSize
EnQueue和DeQueue分别需要操作尾指针rear的后移:Q.rear=(Q.rear+1)% MaxSize;
和头指针front的后移:Q.front=(Q.front+1)% MaxSize;
-
队列链式存储
队列的顺序存储中循环队列面临的数组溢出问题已解决,现在我们来研究不需要担心队列长度的链式存储结构;
具体实现代码在库Data-Structures
-
队列应用
-
报数问题
/* #描述: n个人,从左到右编号1~n,从左到右报数‘1,2,1,2’,报数为‘1’的出列, ‘2’的站到队伍最右端,如此反复,直到n个人全部出列,求它们的出列顺序 #思路: 将n个元素进队列,Dequeue一个元素,它的下一个元素Dequeue并Enqueue 直到直到n个人全部出列 */ void number(int n) { Queue<Integer> queue = new LinkedList<Integer>() ; //将n个元素进队列 for (int i = 1; i <= n; i++) queue.offer(i); System.out.println("出列顺序:"); int a,b; while (!queue.isEmpty()) { a = queue.poll(); System.out.print(a+" "); if (!queue.isEmpty()) { b = queue.poll(); queue.offer(b); } } }
-
约瑟夫问题
/* #描述: n个人围成一个圈,每个人分别标注为1、2、...、n,要求从1号从1开始报数,报到k的人出圈, 接着下一个人又从1开始报数,如此循环,直到只剩最后一个人时,该人即为胜利者。 #思路: 思路与报数问题其实是一致的,只不过要处理的循环数从2变为k */ void number(int n,int k) { Queue<Integer> queue = new LinkedList<Integer>() ; //将n个元素进队列 for (int i = 1; i <= n; i++) queue.offer(i); int a=0;//胜利者 while (!queue.isEmpty()) { for (int i = 1; i < k; i++) { a = queue.poll(); queue.offer(a); } a = queue.poll(); } System.out.println(a); }
-
迷宫问题
-
-

