树

• 树的概况

  • 树的深度/高度：就是树的层数；
  • 树的度：树中所有结点的度的最大值；
  • 结点的度：结点所拥有子树的个数；
  • 叶结点：度为零的结点，也称终端结点或叶子 ；
  • 分支结点：度不为零的结点，也称非终端结点；
  • 有序树：树中各结点的子树是按照从左到右有序排列的，即各子树的位置不能交换；
  • 森林：m（m≥0）颗互不相交的树的集合；

• 树是一种非线性结构，要在计算机实现就得转换为线性结构

  ---

  ​

• 二叉树

  • 定义：每个结点最多有两棵子树的有序树；
  • 满二叉树：二叉树的所有分支结点都有左子树和右子树，并且所有叶子结点都在二叉树的最下一层；是完全二叉树特殊一种
  • 完全二叉树：具有n个结点的完全二叉树，它的结构与满二叉树的前n个结点的结构相同

  ​

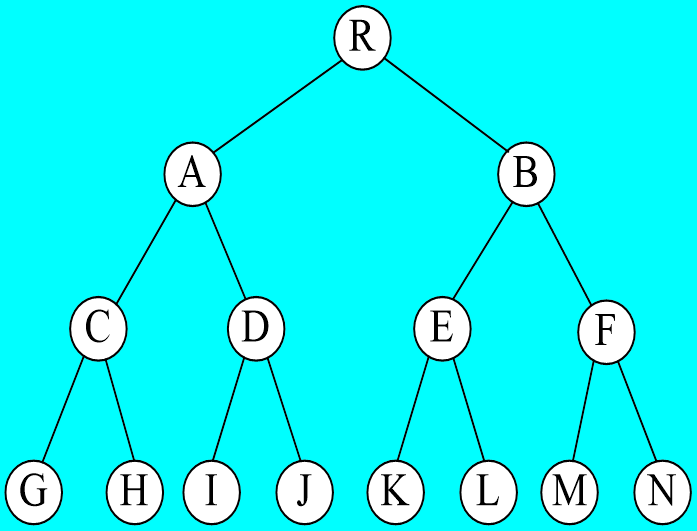  满二叉树
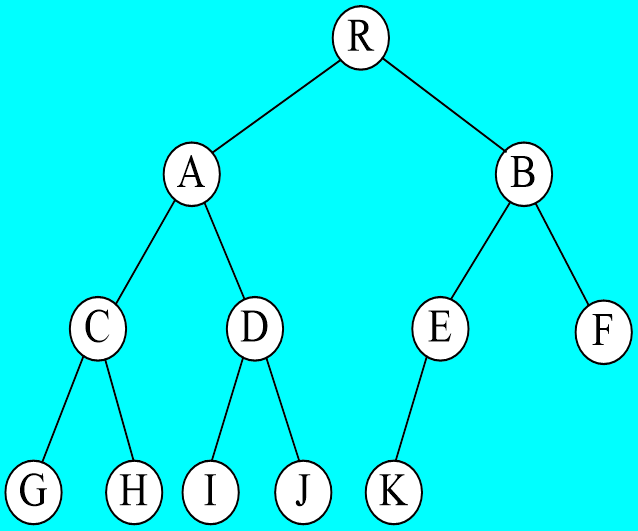  完全二叉树

• 二叉树性质

  • 性质1：非空二叉树的第i(i≥1)层上最多有个结点；

  • 性质2：深度为h (h≥1)的非空二叉树最多有个结点；

  • 性质3：非空二叉树上的终端结点（叶结点）等于双分支结点数加1：

     n0 =  n2 + 1
    

  • 性质4： 具有n（n>0）个结点的完全二叉树的深度

  • 性质5：

    对于具有n个结点的完全二叉树，如果按照从上至下，每层从左至右的次序，对结点进行编号，则编号为 i 的结点有以下性质：

    • 若编号为 i 的结点满足：i≤ n/2 ，即2i≤n，则该结点为分支结点，否则为叶子结点；
    • 若n为奇数，则树中每个分支结点既有左孩子又有右孩子；若n为偶数，则编号 最大的分支结点(编号为n/2)只有左孩子，没有右孩子，其余分支结点左、右孩子都有；
    • 若编号为i的结点有左孩子，则左子结点的编号为2i；若编号为i的结点有右孩子则右子结点为2i+1；
    • 除树根结点外，若一个结点的编号为i，则它的双亲结点的编号为i/2 ；

• 二叉链表

  ​ 由于二叉树顺序存储适用性不强，所以采用二叉链表，其结构定义代码如下:

     typedef struct Node{		
     	ElemType	data;    //数据域	
     	struct Node *lchild;
     	struct Node *rchild; //结点的左右子树指针	
     }BTNode;//二叉树结点类型
  

• 二叉树遍历：前序、中序、后序；

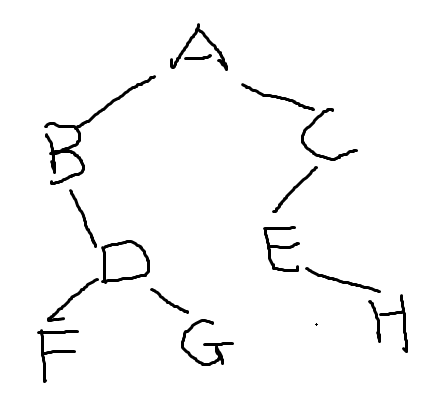
 前序：ABDFGCEH
 中序：BFDGAEHC
 后序：FGDBHECA

• 前序遍历算法：

    //前序遍历二叉树
    void PreOrder(BTNode* root)
    {
    	if (root != NULL) {
    		cout << root->data;  //访问根
    		PreOrder(root->lchild); 	//前序遍历左子树
    		PreOrder(root->rchild);   //前序遍历右子树
    	}
    }
  

  ​

• 二叉树建立

  说了这么多操作，但是要怎么建立二叉树呢？又要建立什么呢？我们当然可以用思路最简单的方法，构建所有节点并连接它们，也可以用中序结合前序/后序 来将一棵树还原出来，但这样做效率显然不高且麻烦；其实我们可以采用保留空指针（设为“#”）的前序来还原树，思路代码如下：

    //按照前序遍历序列建立二叉树
    void CreateBTree_Pre(BTNode* &root, ElemType Array[])
    {	//这里root采用指针引用，是为了改变root也就是建树，以便外部函数调用
    	static int count = 0;	//静态变量count，不会因为递归而重新初始化 ######
    	char item = Array[count];//读取Array[]数组中的第count个元素
    	count++;
    	if (item == '#') //如果读入#字符，创建空树
    	{
    		root = NULL; return;
    	}
    	else
    	{
    		root = new BTNode;
    		root->data = item;
    		CreateBTree_Pre(root->lchild, Array); //建左子树 
    		CreateBTree_Pre(root->rchild, Array); //建右子树 
    	}
    }
  

  • 思考：编程实现二叉树反转？Invert Binary Tree(google)

    ---

• 线索二叉树

  • 所谓的线索二叉树就是将之前左右孩子是null的利用起来，将其设置为前驱后继

  • 按前序遍历序列建立二叉树，请根据前序序列画出此二叉树。

    前序序列为： AB#CD##E##F#G##

    

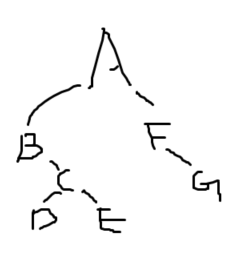
    此二叉树的中序遍历序列为 BDCEAFG，后序遍历序列为 DECBGFA

    请画出此棵树的中序线索二叉树、前序线索二叉树和后序线索二叉树。

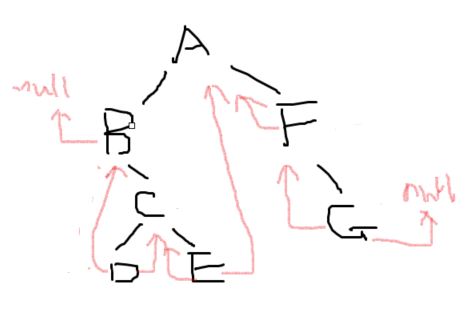    中序线索二叉树

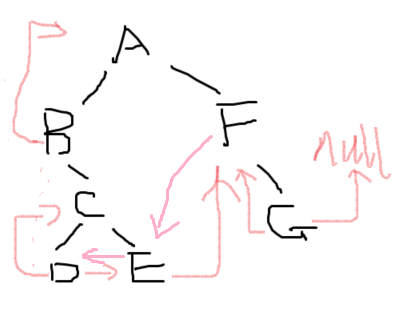    前序线索二叉树

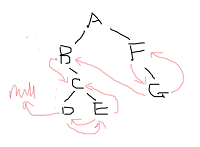    后序线索二叉树

• 哈夫曼树