穷竭搜索是将所有的可能罗列出来,在其中找出答案的方法。其主要有深度优先搜索(DFS)和 广度优先搜索(BFS)。
- 深度优先搜索(DFS)
定义:它表示从某个状态开始,不断转移状态直到无法转移,然后退回到前一步的状态,继续转移到其他状态,如此不断重复,直到找到最终的解。
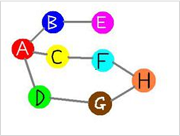
举例说明:下图是一个无向图,如果我们从A点发起深度优先搜索(以下的访问次序并不是唯一的,第二个点既可以是B也可以是C,D),则我们可能得到如下的一个访问过程:A->B->E(没有路了!回溯到A->C->F->H->G->D(没有路,最终回溯到A,A也没有未访问的相邻节点,本次搜索结束)。
例题1:
部分和问题
描述
给定整数a1、a2、.......an,判断是否可以从中选出若干数,使它们的和恰好为K。
输入
首先,n和k,n表示数的个数,k表示数的和。
接着一行n个数。
(1<=n<=20)
输出
如果和恰好可以为k,输出“YES”,并按输入顺序依次输出是由哪几个数的和组成,否则“NO”
样例输入
4 13
1 2 4 7
样例输出
YES
2 4 7
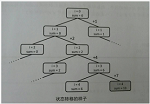
很明显该题完全符合DFS,我们只需要考虑是否选择该数?然后不断转移,找到答案为止,思路的过程如下图:
代码:
int n,k,a[20],b[20];
void solve(){//部分和问题
bool dfs(int i,int sum);
scanf("%d%d",&n,&k);
for(int i=0;i<n;++i){
scanf("%d",&a[i]);
}
if(dfs(0,0))printf("Yes\n");
else printf("No");
for(int i=0;i<n;++i){
if(b[i]) printf("%d ",a[i]);
}
}
bool dfs(int i,int sum){
//如果前n项都已经计算过,返回sum与k是否相等
if(i==n){return sum==k;}
//不选择a[i]
if(dfs(i+1,sum)){
b[i]=0;
return true;
}
//选择a[i]
if(dfs(i+1,sum+a[i])){
b[i]=1;
return true;
}
//以上情况都不满足便返回false
return false;
}
例题2:
Lake Counting(POJ No.2386)
描述
Due to recent rains, water has pooled in various places in Farmer John's field, which is represented by a rectangle of N x M (1 <= N <= 100; 1 <= M <= 100) squares. Each square contains either water ('W') or dry land ('.'). Farmer John would like to figure out how many ponds have formed in his field. A pond is a connected set of squares with water in them, where a square is considered adjacent to all eight of its neighbors.
Given a diagram of Farmer John's field, determine how many ponds he has.
输入
* Line 1: Two space-separated integers: N and M
* Lines 2..N+1: M characters per line representing one row of Farmer John's field. Each character is either 'W' or '.'. The characters do not have spaces between them.
输出
* Line 1: The number of ponds in Farmer John's field.
样例输入
10 12
W........WW.
.WWW.....WWW
....WW...WW.
.........WW.
.........W..
..W......W..
.W.W.....WW.
W.W.W.....W.
.W.W......W.
..W.......W.
样例输出
3
题目的大概意思就是雨后积水,要求有多少处水洼,上面样例可以直观的看出有三处,该题的思路:就是用‘.’代替‘w’,一次DFS后与初始这个‘w’相连的所有‘w’都会被替代成‘.’;以此类推,总共进行的DFS次数就是答案了。
代码:
int n=10,m=12;
char a[10][13] = {
"W........WW.",
".WWW.....WWW",
"....WW...WW.",
".........WW.",
".........W..",
"..W......W..",
".W.W.....WW.",
"W.W.W.....W.",
".W.W......W.",
"..W.......W."
};
void solve(){
void dfs(int,int);
int res=0;
for(int i=0;i<n;++i){
for(int j=0;j<m;++j){
if(a[i][j]=='W'){
dfs(i,j);
++res;
}
}
}
printf("%d\n",res);
}
void dfs(int i,int j){
a[i][j]='.';//将当前该值代替为'.'
//接下来循环遍历与其相邻的八个方向
for(int dx=-1;dx<=1;++dx){
for(int dy=-1;dy<=1;++dy){
int x=i+dx,y=j+dy;
//确保数组不越界
if(0<=x&&x<n && 0<=y&&y<m &&a[x][y]=='W'){
dfs(x,y);
}
}
}
}
- 广度优先搜索(BFS)
定义:广度优先搜索(也称宽度优先搜索)是连通图的一种遍历策略。因为它的思想是从一个顶点V0开始,辐射状地优先遍历其周围较广的区域,故得名。
举例说明:同样引用该图,如果我们从A点发起广度优先搜索,那么第一次BFS就会从A ->B、A->C和A->D,呈现辐射散开形状,而第二次BFS则会从B、C、D这三个点开始散开来,直到找到最终解。

例题:
迷宫的最短路径
描述
给定一个大小为N*M的迷宫,由通道('.')和墙壁('#')组成,其中通道S表示起点,通道G表示终点,
每一步移动可以达到上下左右中不是墙壁的位置。试求出起点到终点的最小步数。(N,M<=100)
输入
10 10
#S######.#
......#..#
.#.##.##.#
.#........
##.##.####
....#....#
.#######.#
....#.....
.####.###.
....#...G#
输出
22
思路: 求取最短路时,DFS需要反复经过同样的状态,所以此时应采用BFS;
- DFS和BFS的比较: 顾名思义,DFS就像一个猛汉一根筋地闯荡寻找宝藏,这条路找不到就返回原点,重新规划另一条路,不断循环该过程,直至找到宝藏;而BFS更像是一个寻宝团伙,分路出发,一层一层寻找,直至找到相对最优的宝藏路线。 两者都会生成所有能够遍历到的状态,DFS更倾向于目标比较明确,例如找到宝藏就好,而BFS更适合在不断扩大遍历范围时找到最优解。它们的时间复杂度是一样的,没有优劣之分,只是视不同情况选择不同算法。 当然,BFS会把状态逐个加入队列,因此通常需要与状态数成正比的内存空间。反之DFS与最大的递归深度成正比,一般与状态数相比,递归深度并不会太大,所以可以认为DFS比BFS更加节省内存。

