图

• 图：图G由集合V和集合E组成，记为 G＝(V，E)，其中：V是顶点元素的有限集合，E是顶点间关系，有箭头的为有向图；

• 图的存储结构

  • 邻接矩阵

    特点：#无向图的邻接矩阵对称

    //邻接矩阵类型
    typedef struct {
    	weight  arcs[MAXV][MAXV]; //邻接矩阵
    	ElemType  data[MAXV];//一维数组顶点表
    	int n;//顶点个数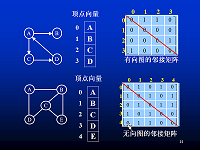
    };
    

    

    ​

  • 邻接表（n由顶点表和边表组成，是链式存储结构）

    头结点和边结点结构如下：

    

    

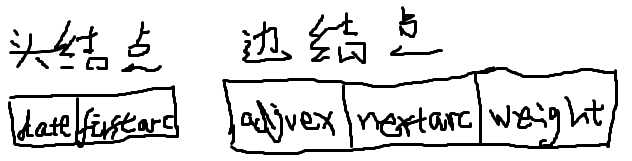
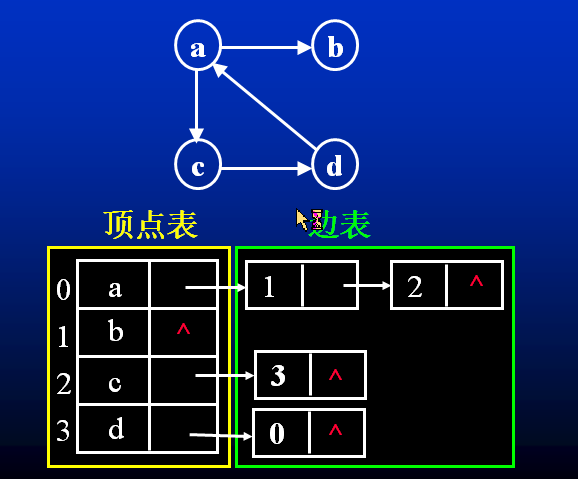
    注意：边结点表顺序是随意的

    //图的完整邻接表存储类型
    typedef struct ANode{
        int adjvex; //该边的邻接点编号
      	struct ANode *nextarc; //指向下一条边的指针
      	int weight； //该边相关信息，如权值等
    } ArcNode;
    //
    typedef int InfoType;
    typedef struct Vnode{
        InfoType info; //顶点的其他信息
      	ArcNode *firstarc; //指向第一个边结点
    } VNode;
    typedef struct{
        VNode adjlist[MAXV]; //邻接表头结点数组
        int n,e; //顶点数n和边数e
    } AdjGraph;
    

    ​

---

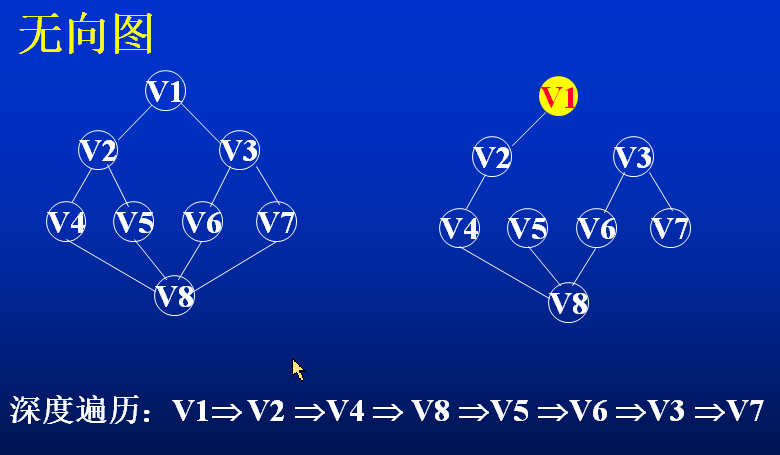
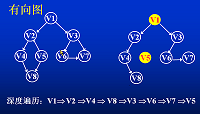
• DFS

  从图的某一顶点V出发（起点任选），访问此顶点；然后依次从V的未被访问的邻接点出发，深度优先遍历图，直至图中所有和V相通的顶点都被访问到；若此时图中尚有顶点未被访问，则另选图中一个未被访问的顶点作起点，重复上述过程，直至图中所有顶点都被访问为止。

  

  

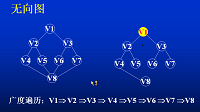
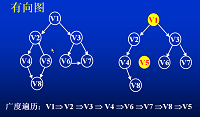
• BFS

  从图的某一顶点V出发（起点任选），访问顶点；再依次访问V的各个未曾访问过的邻接点；然后分别从这些邻接点出发，依次访问它们的邻接点，并使“先被访问的顶点的邻接点”先于“后被访问的顶点的邻接点”被访问。直至图中所有已被访问的顶点的邻接点都被访问到。若此时图中尚有顶点未被访问，则另选图中一个未被访问的顶点作起点，重复上述过程，直至图中所有顶点都被访问为止。

  

  

---

• 利用图的邻接矩阵来构建、遍历图

  #define MAXV 7//最大顶点个数

  typedef int weight;//邻接矩阵元素类型
  typedef char ElemType;//顶点数据元素类型

  //邻接矩阵类型
  typedef struct {
  	weight  arcs[MAXV][MAXV]; //邻接矩阵
  	ElemType  data[MAXV];//一维数组顶点表
  	int n;//顶点个数
  } MGraph, *AdjMatrix;

  //创建邻接矩阵, g是指向图的指针变量，m[][MAXV]是邻接矩阵，d[]是顶点表,n顶点个数
  void CreateGraph(AdjMatrix g, int m[][MAXV], ElemType d[], int n);

  //	#####利用DFS和邻接矩阵实现对图的遍历#####
  //取顶点v的第一个邻接点
  int GetFirst(AdjMatrix g, int v);

  //取顶点v的位于顶点t之后的下一个邻接点
  int GetNext(AdjMatrix g, int v, int t);

  //以顶点v为起点，深度优先遍历图
  void DFS(AdjMatrix g, int v, int visited[]);

  //第二种DFS遍历方法（推荐）
  void iDFS(AdjMatrix g, int v,int ivisited[])
  {
  	ivisited[v] = 1;
  	cout << g->data[v];
  	for (int  i = 0; i <g->n; i++)
  		if (g->arcs[v][i]==1 && ivisited[i]==0) 
  			iDFS(g,i, ivisited);
  }
  //定义一维数组ivisited并初始化，作为访问标记。
  void iDFSTraverse(AdjMatrix g,int v,int ivisited[])
  {
  	for (int i = v; i < g->n; i++)
  	{
  		if (ivisited[i]==0)
  			iDFS(g,i, ivisited);
  	}
  }

#具体代码#

• 邻接矩阵转换为邻接表

  void MatToList(MGraph g, ALGraph *&G)
  //将邻接矩阵g转换成邻接表G
  {
    	int i, j, n = g.n;			//n为顶点数
  	ArcNode *p;
  	G = (ALGraph *)malloc(sizeof(ALGraph));
    for (i = 0; i<n; i++)			//给邻接表中所有头结点的指针域置初值
  		G->adjlist[i].firstarc = NULL;
  	for (i = 0; i<n; i++)		//检查邻接矩阵中每个元素
  		for (j = n - 1; j >= 0; j--)
  			if (g.edges[i][j] != 0)	 //邻接矩阵的当前元素不为0
  			{
  				p = (ArcNode *)malloc(sizeof(ArcNode));	//创建一个结点*p
  				p->adjvex = j;
  				p->info = g.edges[i][j];
  				p->nextarc = G->adjlist[i].firstarc;//采用头插法插入*p
  				G->adjlist[i].firstarc = p;
  			}
  	G->n = n; G->e = g.e;
  }
  
  void DispAdj(ALGraph *G)
  //输出邻接表G
  {
  	int i;
  	ArcNode *p;
  	for (i = 0; i<G->n; i++)
  	{
  		p = G->adjlist[i].firstarc;
  		printf("%3d: ", i);
  		while (p != NULL)
  		{
  			printf("%3d", p->adjvex);
  			p = p->nextarc;
  		}
  		printf("\n");
  	}
  }
  

  ​

• 利用BFS和邻接表实现对图的遍历

---

图的应用

• ​
• ​